第 D 部分：求解器稳定性/网格划分

本节聚焦于求解器稳定性与网格选择。一维（1D）仿真通常非常稳定且运行快速。随着维度从 1D 增加到 2D 和 3D，方程数量以及它们之间的耦合项数量都会增长，从而更容易出现数值不稳定。如果在 2D 或 3D 仿真中未谨慎选择设置，仿真可能无法收敛。

这里我们将有意推动几个简单设置以触发不收敛，然后诊断其原因以及如何修复。通过亲自复现实这些常见失败模式，你将学会识别症状并应用正确的补救措施（例如调整网格、减小偏置步长，或缓和极端材料参数）以恢复稳定解。

1. 不现实的低数值

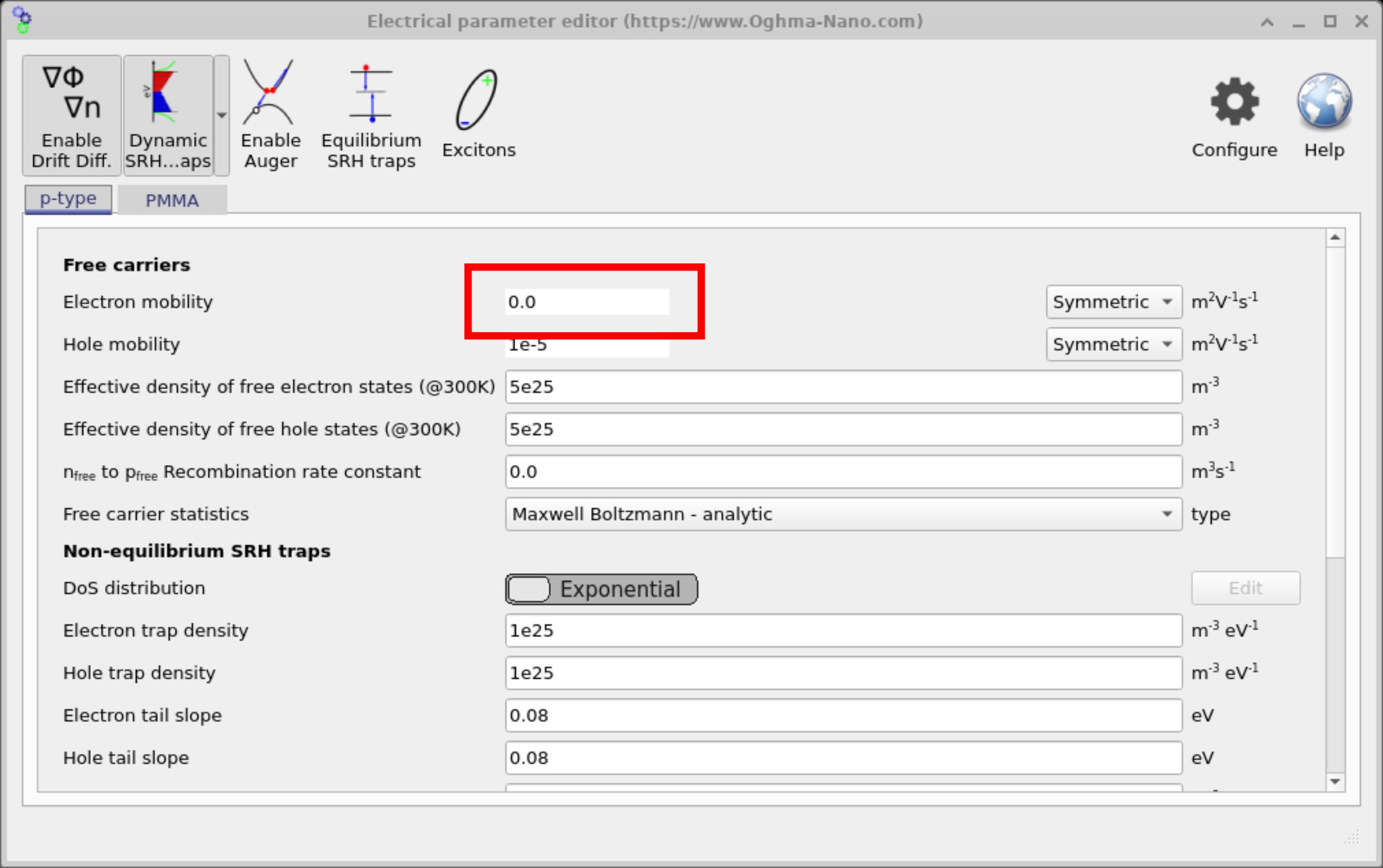
在许多情况下，收敛问题源于非物理输入值。为说明这一点，我们故意将载流子迁移率设置为 0 并检查由此产生的错误。当然，在真实材料中迁移率不可能真正为零——它总是有限值——但该示例展示了当求解器接收到不现实参数时会发生什么。

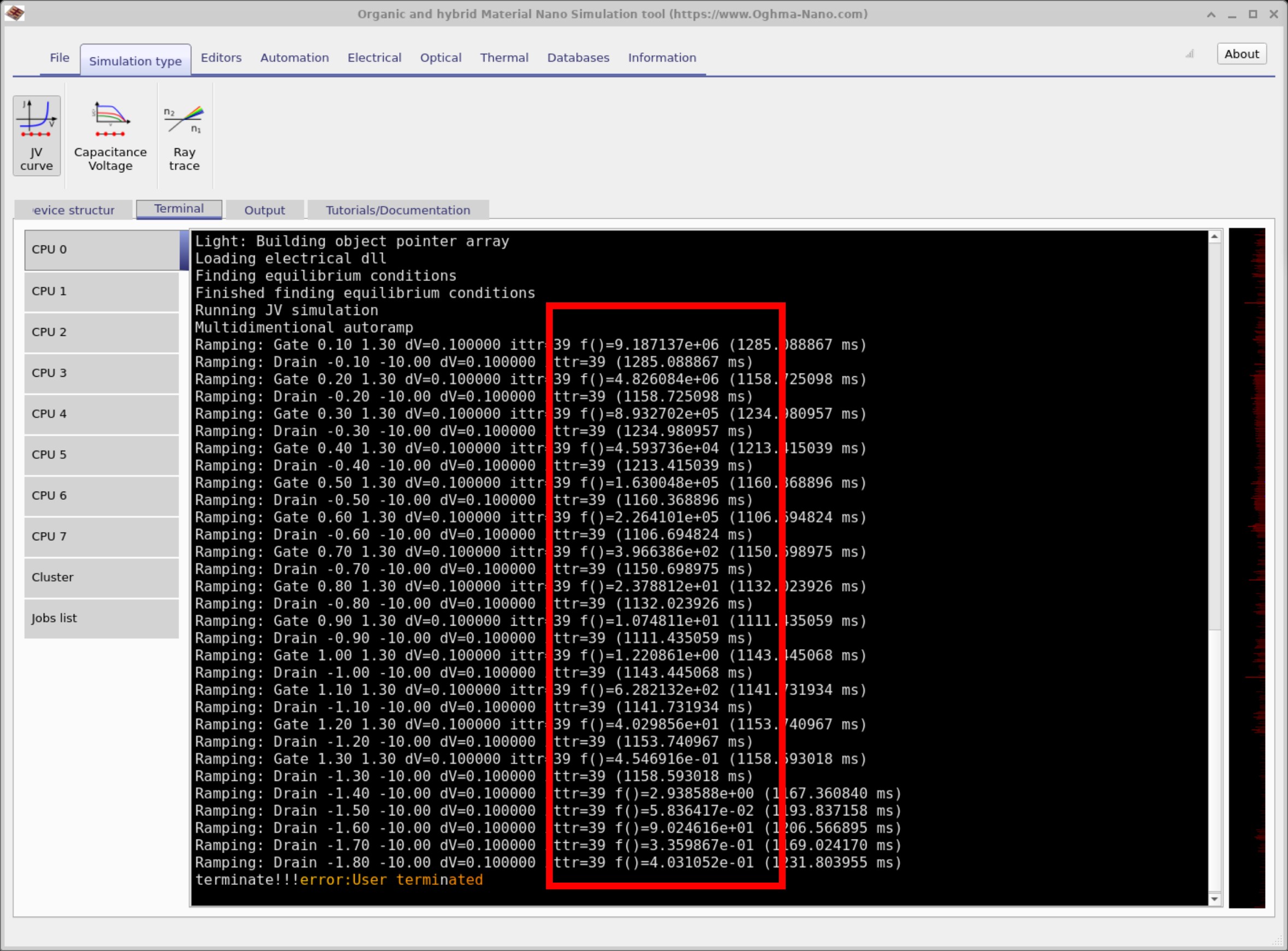
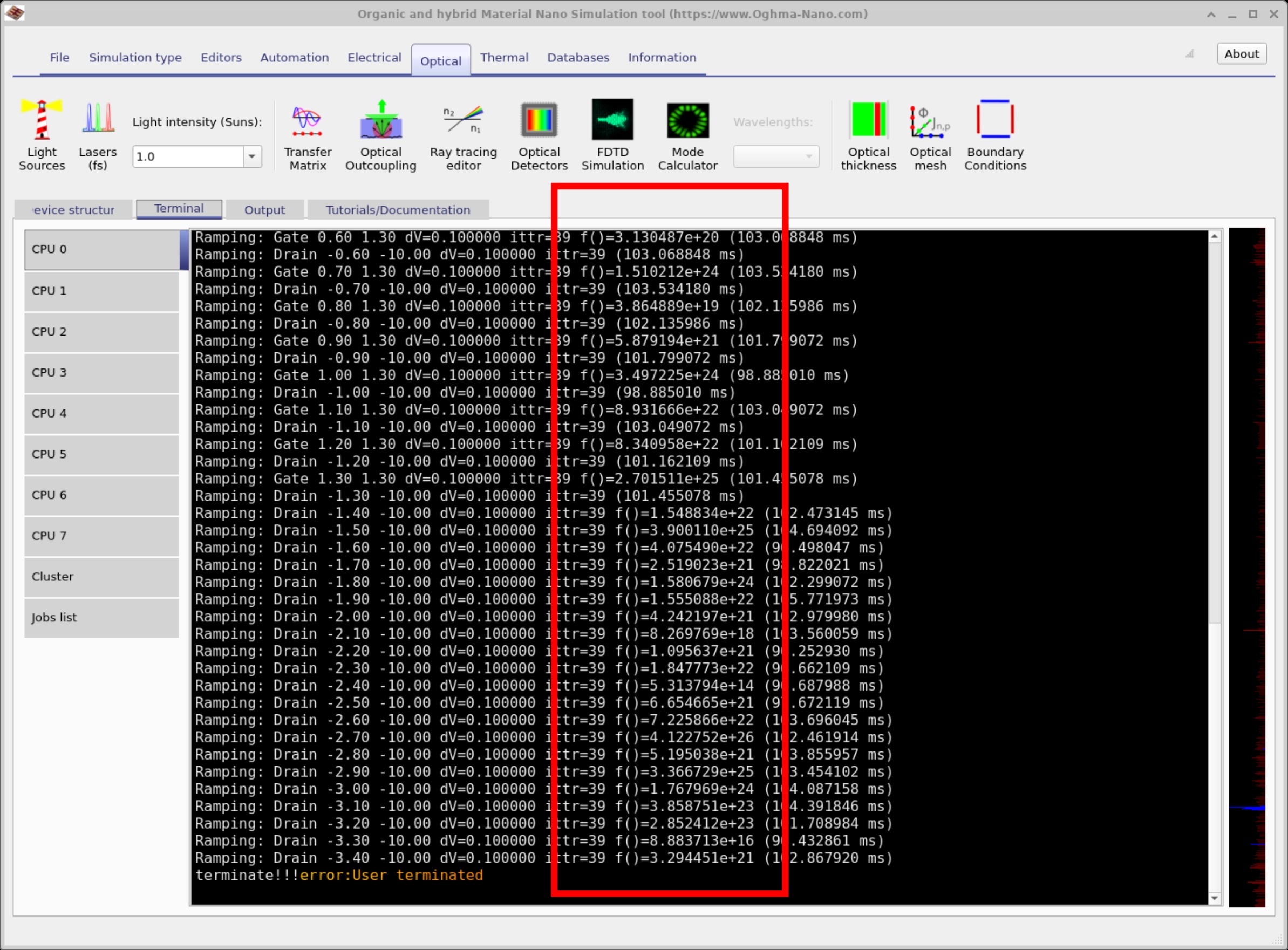
打开 Electrical Parameters 编辑器（主窗口 → Device 选项卡）并将迁移率设置为 0，如 ?? 所示。现在运行仿真。你应当看到类似于 ?? 的错误界面，其中有两个红色框：一个竖框圈住残差汇总，另一个横框靠近崩溃信息。

如果你查看竖向红框，可以看到 f()=2.54e2，后面还有其他行，其中 f() 非常大（例如 1e15、1e5、1e8、1e7）。这里，f() 是求解器 残差误差：衡量当前耦合方程满足程度的指标。理想情况下，求解器残差应当为零，尽管在实践中这不可能完全实现。残差在 1e−10 到 1e−8 的范围表示收敛非常好，而 1e−1 左右仍然可以接受。 相比之下，达到数百（例如 2.54e2）的残差——尤其当伴随分量值高达 1e15 时——清楚表明求解器正在吃力，系统已经变得不稳定。

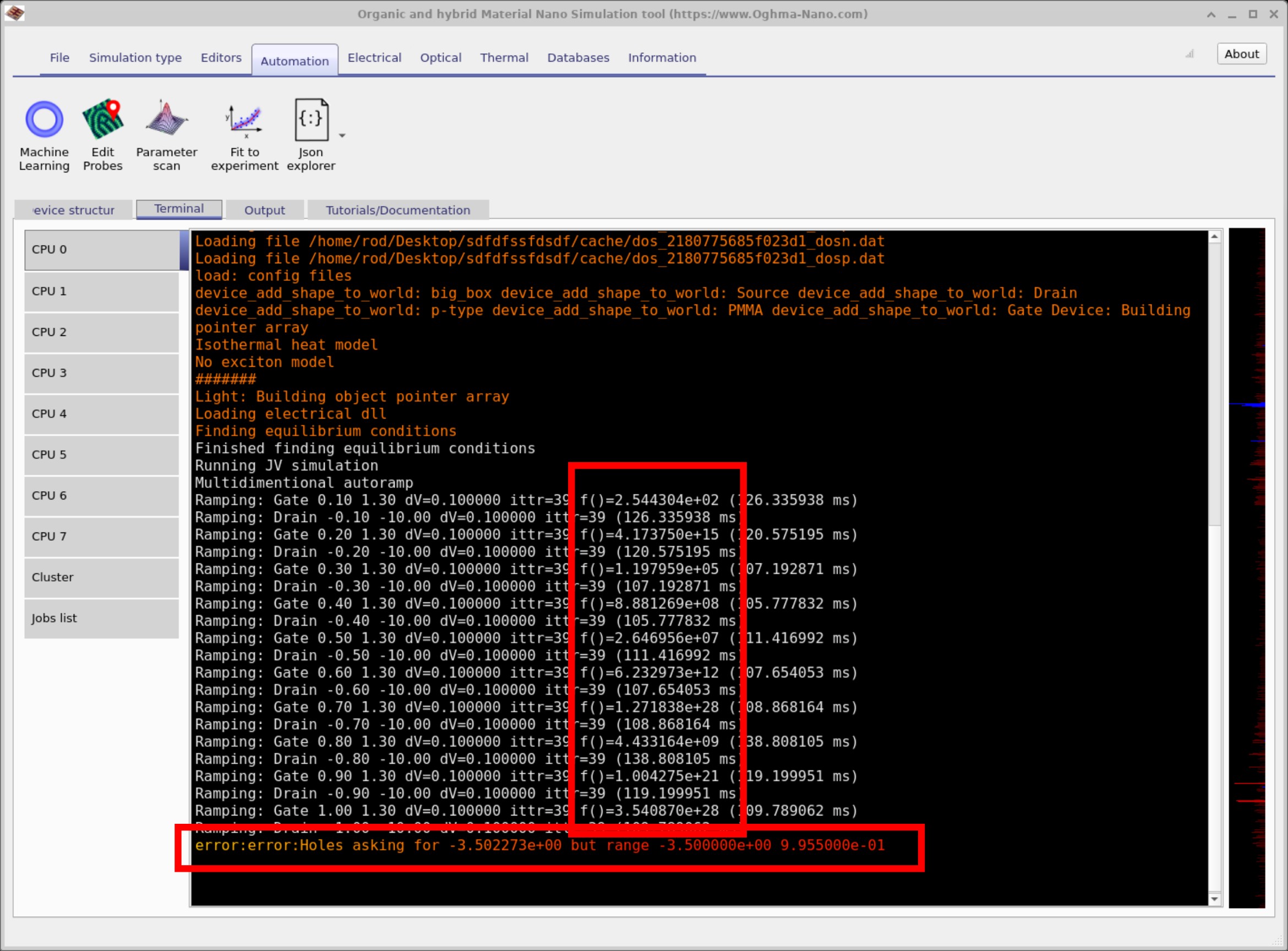
横向红框通常会报告运行最终中止的原因：Holes asking for 3e5 but only defined in range [min, max]. 这意味着计算得到的准费米能级已超出表格化范围。在开始之前，模型会在较大的能量范围内预先表格化诸如准费米能级与载流子浓度之间的关系——确实比通常在器件中预期出现的范围大得多。当求解器变得不稳定时，模型可能会请求超出该范围的非现实数值；此时求解器无法评估所需量并停止。

简而言之，通过将迁移率设为非物理值（μ = 0），我们迫使方程进入一个毫无物理意义的区域，因此数值方法失败：出现巨大残差，随后请求超出预计算表的数值，进而崩溃。需要强调的是，这并不是模型的弱点或软件错误。 当输入非物理参数时，求解器会被推入一个不存在数学或物理有效解的区域，因此无法给出有意义的结果。

2. 不现实的高数值

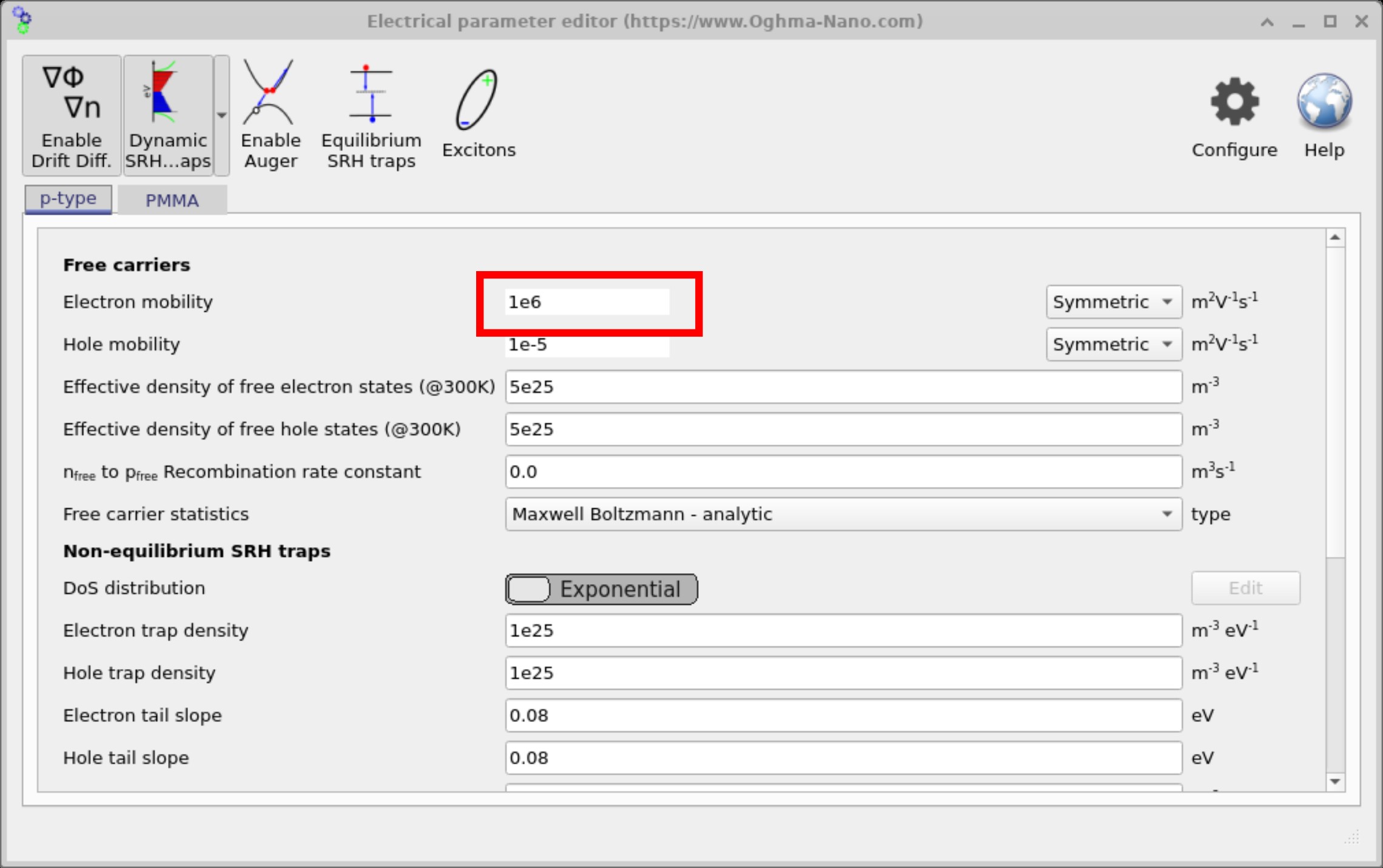
在该示例中，我们将载流子迁移率设置为 μ = 1×106 m²·V⁻¹·s⁻¹。这对半导体 drift–diffusion 模型而言是一个刻意设置的非物理数值：如此量级更可能与金属导电区域相关，而不是有机或典型半导体中的跳跃/能带输运。在实际 OFET 仿真中，你不会使用如此大的数值。

若使用该设置运行仿真，你可以观察到求解器难以收敛。在残差读出（报告 f() 的框）中，你会看到极其巨大的误差——例如 1e24、1e19、1e21——且不会衰减。残差在最初几次迭代中偏高是正常的，因为求解器正在寻找一致的状态，但它们应当很快趋于较小值。持续巨大的残差清楚表明系统由于所选参数而变得数值刚性很强或非物理。

要点：避免不现实的高迁移率。过大的输运系数会使 PDE 系统非常刚性，导致病态条件与不收敛。请为你的材料体系使用物理合理的 μ 值，并采用适度的偏置步进重新运行以恢复稳定行为。

3. 不良器件结构

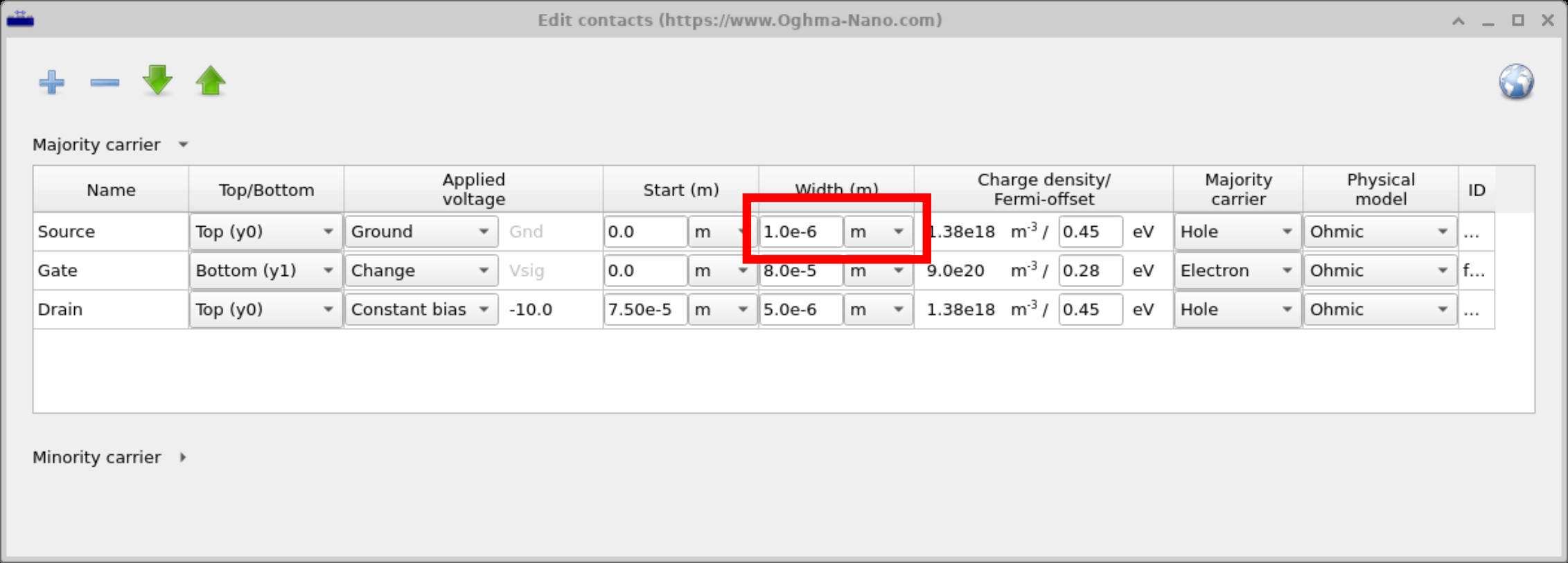
在该示例中，我们打开接触编辑器并将 Source 的接触宽度设置为非常小的值（见 ??），设为一微米。乍看之下这似乎并不成问题，但它会引入一个微妙的问题：仿真基于有限差分网格，电场和载流子密度等量只在定义的网格点上计算。

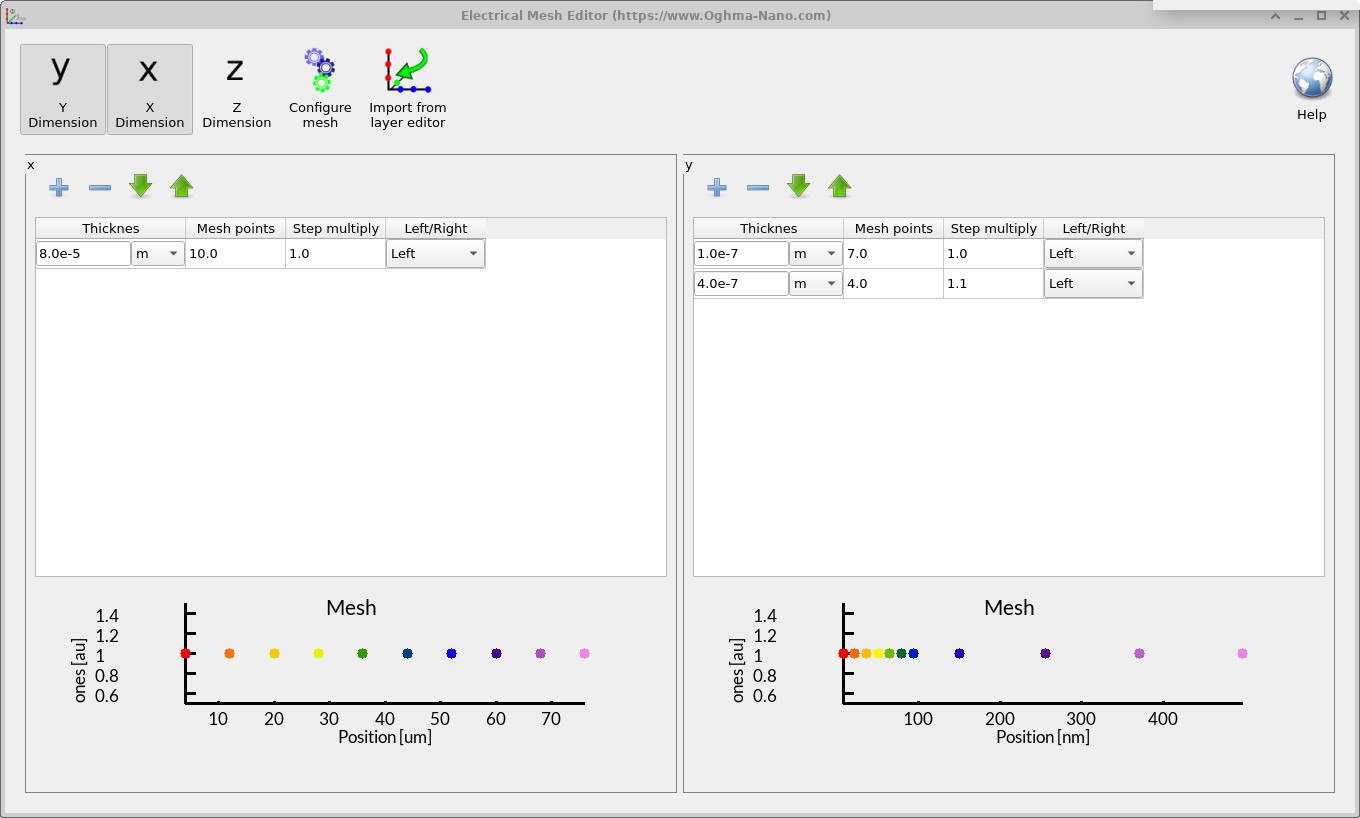
如果你检查 Electrical Mesh Editor（位于 Electrical 选项卡下），你会注意到这个超薄的一微米接触落在网格点之间（见 ??）。因此，该接触在有限差分网格中实际上被“漏掉”，从而从未被正确施加到器件结构中。这会在所定义的几何与数值网格之间产生不匹配，导致仿真无法收敛。

要修复此问题，你可以增大接触的厚度，使其至少覆盖一个网格点，或提高网格密度（即添加更多点），使有限差分网格能够正确捕捉该接触。

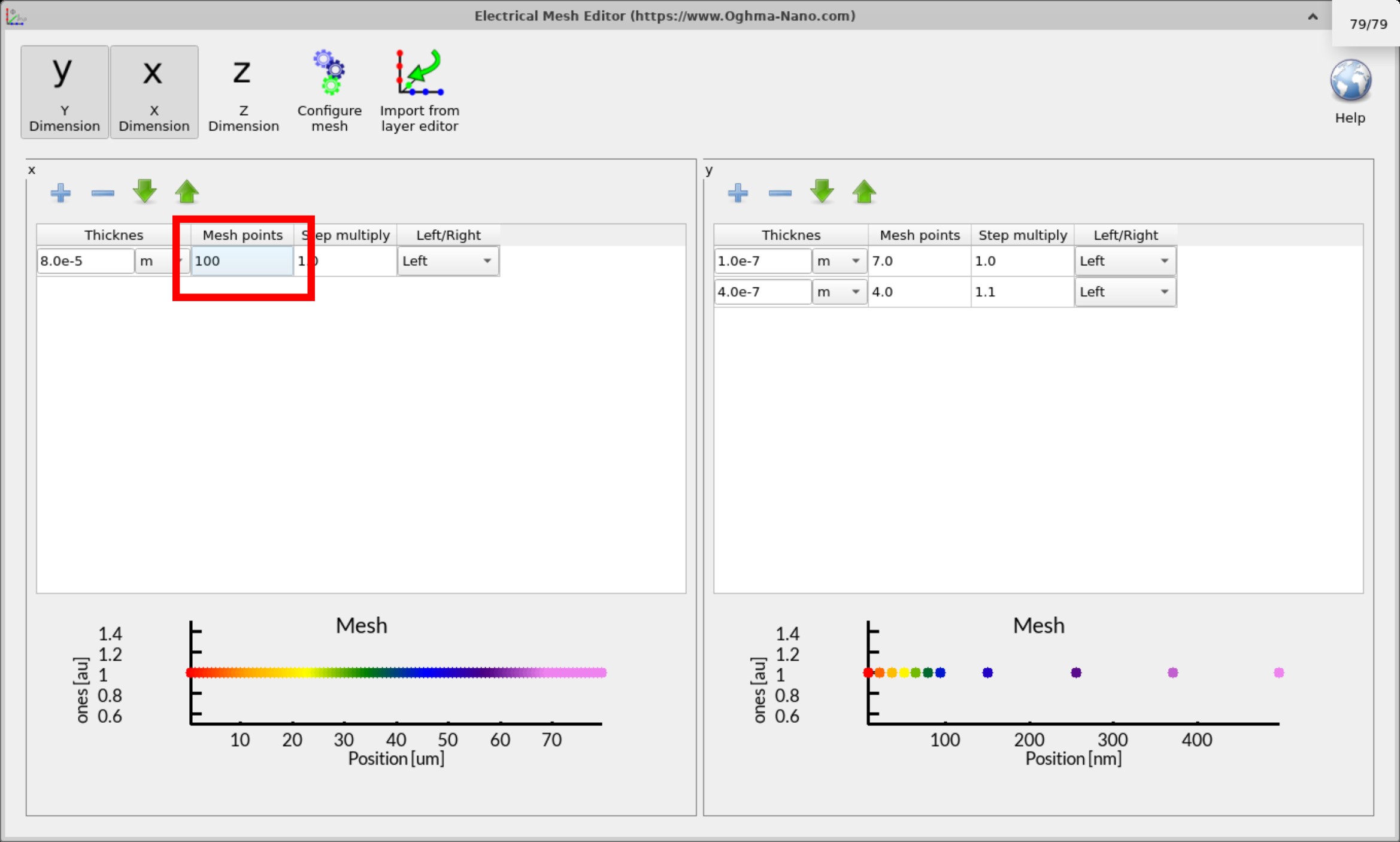
4. 过多的网格点