钙钛矿太阳能电池的 CELIV 测量：第 a 部分

CELIV 测量装置示意图：太阳能电池可选背景光或激光脉冲照明，连接到施加电压斜坡的信号发生器，并由具有 50 Ω 输入电阻的示波器记录瞬态抽取电流。 — CELIV 技术的实验配置。使用信号发生器对太阳能电池施加线性递增的反向偏置。由输入电阻为 50 Ω 的示波器测量得到的抽取电流。可选的背景照明与激光激发可用于在不同条件下探测载流子密度与迁移率。

1. 概述

在本教程中，我们将首先介绍线性递增电压电荷抽取（CELIV）技术的基本概念，概述其如何用于探测薄膜半导体中的载流子迁移率与密度。在建立理论背景之后，我们将快速进入实践步骤，展示如何在 OghmaNano 中配置并运行 CELIV 仿真。该理论与动手仿真的结合将同时提供对方法的清晰理解以及将其应用于你自己器件的工具。

2. CELIV 背景

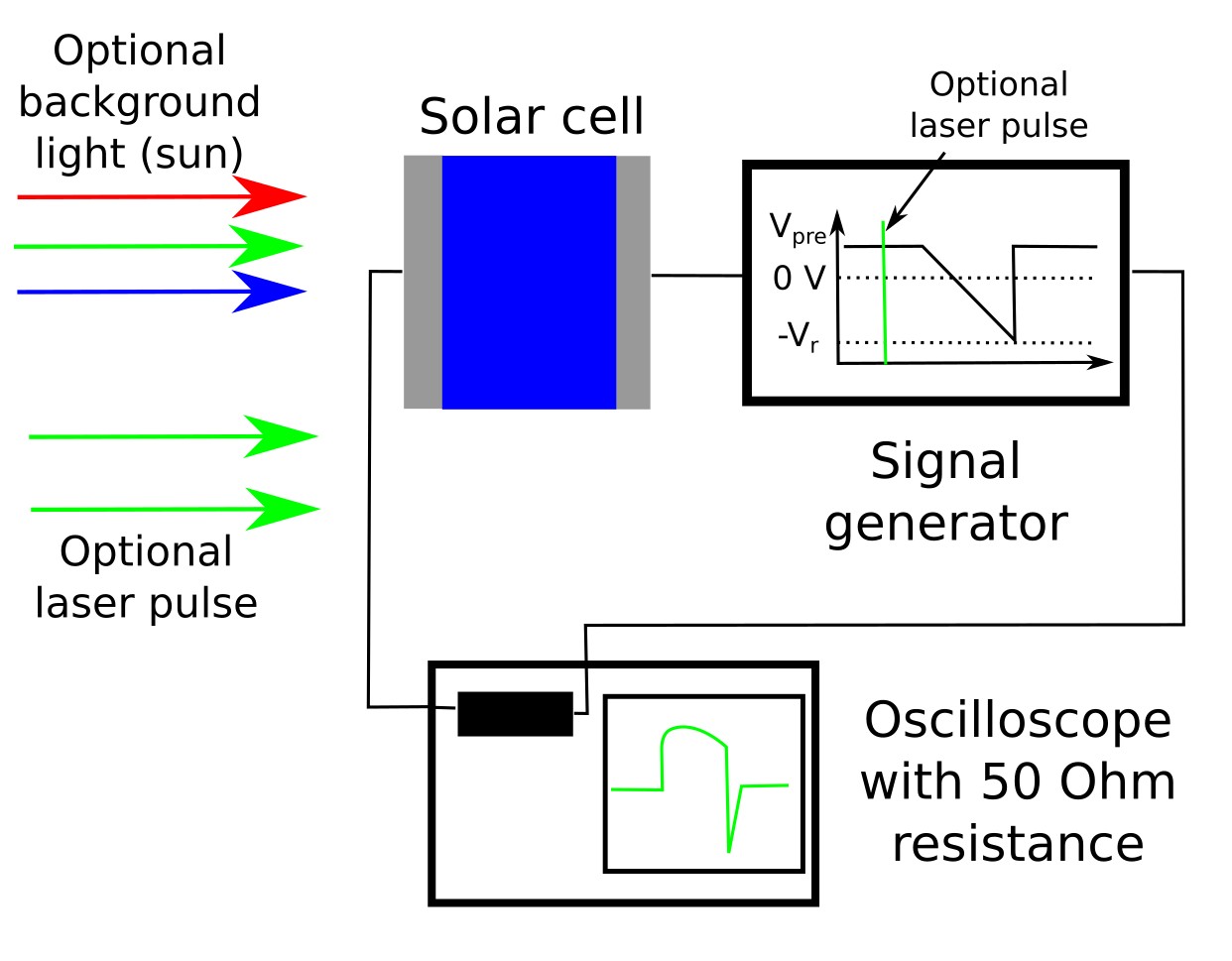
线性递增电压电荷抽取（CELIV）技术是一种实验方法，用于研究有机与钙钛矿太阳能电池中的电荷载流子迁移率与密度。在典型配置中，太阳能电池连接到施加线性递增反向偏置的信号发生器，同时将得到的电流瞬态记录在示波器上。可选的连续照明或短激光脉冲可用于产生电荷载流子。该配置的示意图见 ??。

施加电压斜坡时，测得电流由两个不同贡献组成：来自器件几何电容的矩形基线，以及来自半导体中可移动电荷载流子抽取的附加峰。几何电容项始终存在，而载流子相关峰直接提供迁移率与载流子密度信息。这些电压与电流瞬态的示例见 ??。

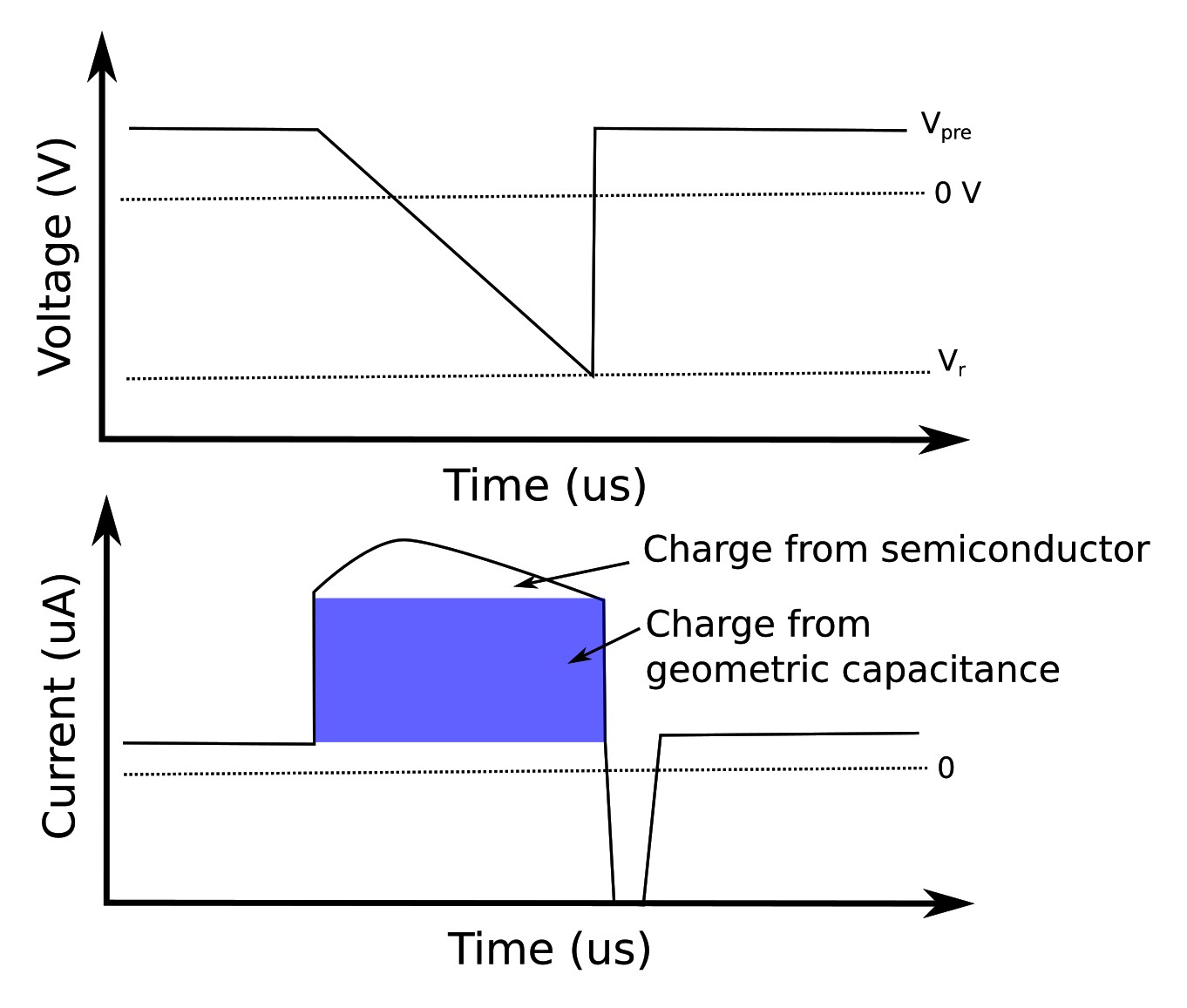
施加的电压斜坡（上）显示从 Vpre 到 Vr 的线性降低，以及对应的抽取电流瞬态（下）。电流由几何电容的矩形贡献与半导体中可移动电荷载流子导致的附加峰组成。 — CELIV 技术中的电压与电流瞬态。施加的电压斜坡（上）驱动载流子抽取。测得电流（下）既包含来自器件几何电容的基线贡献（蓝色区域），也包含来自半导体中可移动电荷的附加峰。该峰的位置与高度用于确定载流子迁移率与密度。

理想 CELIV 抽取与陷阱受限抽取的比较。左：自由电子与空穴被直接抽取，得到尖锐瞬态。右：载流子占据浅、中、深陷阱，导致抽取信号延迟并展宽。 — 理想情况与陷阱受限的 CELIV 抽取。左：在理想情况下，仅抽取自由载流子，产生清晰定义的瞬态。右：当电子与空穴分布在浅、中、深陷阱中时，它们的释放发生在不同时间尺度上。这会导致更慢、展宽的抽取电流，并提供关于半导体中陷阱能量分布的信息。

载流子迁移率可通过测量抽取电流达到最大值的时间从 CELIV 瞬态中直接确定。在均匀载流子分布且复合可忽略的最简单情况下，迁移率由 CELIV 方程给出： \[ \mu = \frac{2 d^{2}}{3 A t_{\text{max}}^{2}} \] 其中 \(d\) 为有源层厚度，\(A\) 为电压斜坡速率（\(A = \mathrm{d}V/\mathrm{d}t\)），\(t_{\text{max}}\) 为电流峰出现的时间。该关系将实验观测到的瞬态与所关注的基本传输参数联系起来。

3. CELIV 局限性

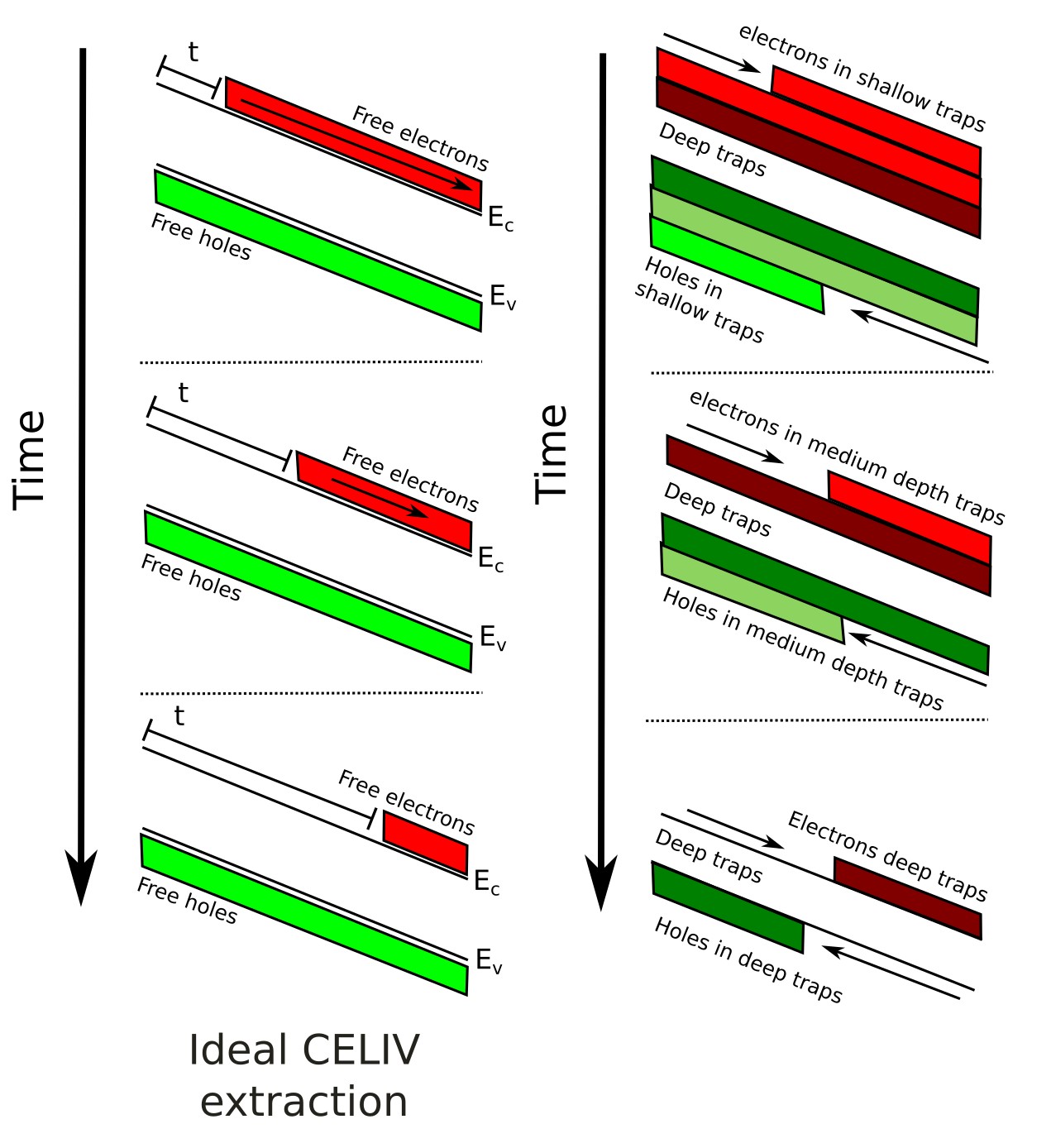
CELIV 迁移率方程的推导依赖若干简化假设。首先，假设仅一种电荷载流子主导传输，因此在施加电压斜坡时只有一种载流子物种运动。其次，假设载流子均匀分布，以类似于 ?? 左侧所示的理想化方式平滑地从器件中滑出。第三，认为抽取过程中复合过程可以忽略，因此不会发生显著的载流子损失。在现实中，这些条件很少被满足。如 ?? 右侧所示，电荷载流子常占据浅、中或深陷阱，其延迟释放会产生展宽或畸变的抽取瞬态。因此，与许多实验技术一样，用 CELIV 提取的迁移率应被视为近似值而非真实的微观值，并且表观迁移率甚至可以在瞬态过程中演化（doi:10.1063/1.4818267）。该局限性在无序有机半导体中尤为重要，因为能量无序与俘获会强烈影响传输。相较之下，钙钛矿材料通常表现出更高的迁移率与更低的陷阱密度，使得标准 CELIV 分析更稳健且更易解读。

💡 检验你的理解： 尝试将 CELIV 理论应用于一个简单用例。

假设你有一个厚度为 d = 200 nm 的器件，电压斜坡速率为 A = 2 × 10⁶ V/s，并且电流峰出现在 t_max = 5 µs。使用 CELIV 迁移率方程，估算载流子迁移率。

显示答案

CELIV 迁移率由下式给出 \[ \mu = \frac{2 d^{2}}{3 A t_{\text{max}}^{2}} \] 代入数值： d = 200 × 10^-9 m， A = 2 × 10⁶ V/s， t_max = 5 × 10^-6 s。

\[ \mu = \frac{2 (200 × 10^{-9})^{2}}{3 (2 × 10^{6}) (5 × 10^{-6})^{2}} \approx 1.1 × 10^{-4} \; \text{cm}^2/\text{Vs} \]

这个简单示例表明，CELIV 瞬态中的峰值时间可以转换为迁移率估算值。

4: 在 OghmaNano 上运行 CELIV 仿真

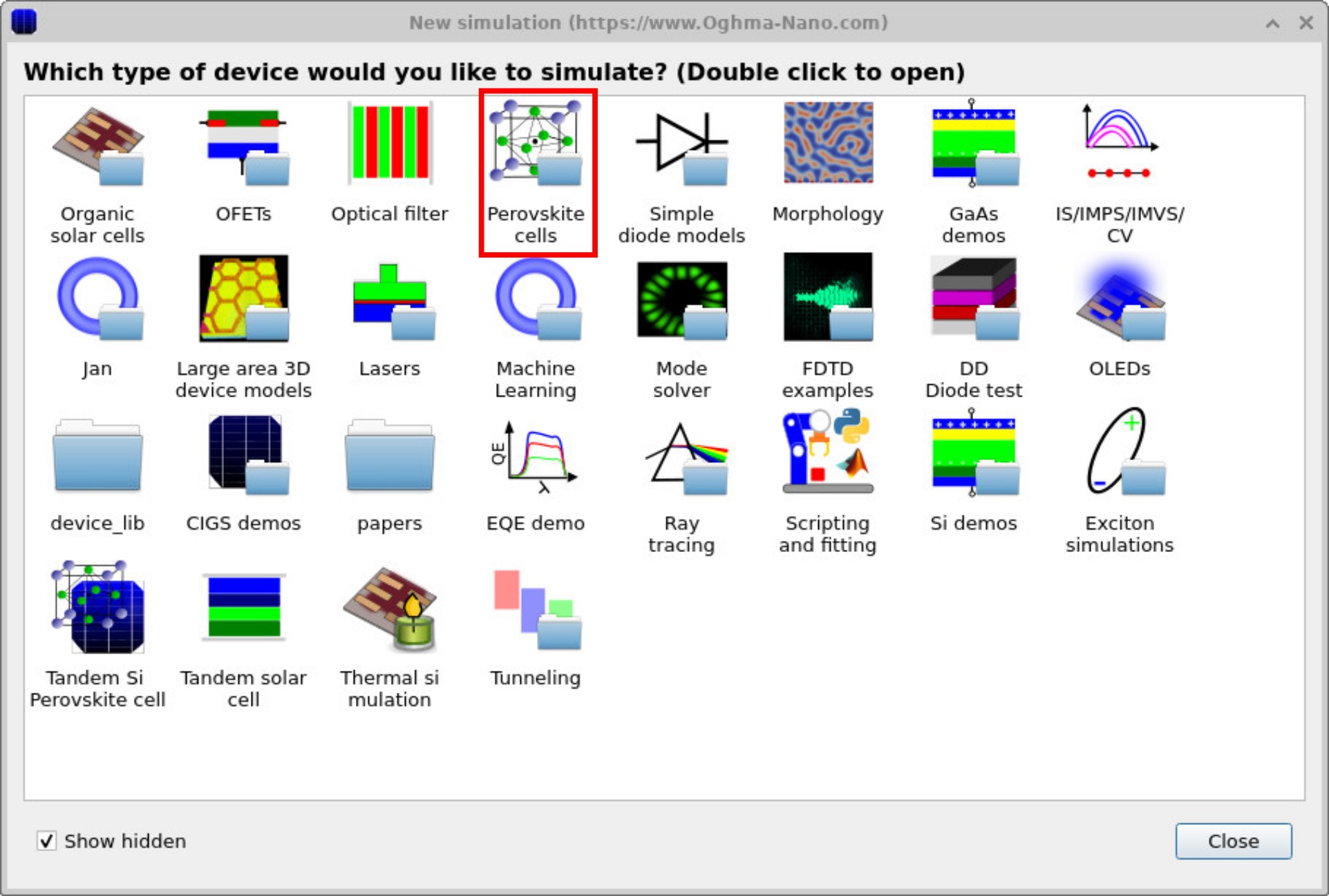
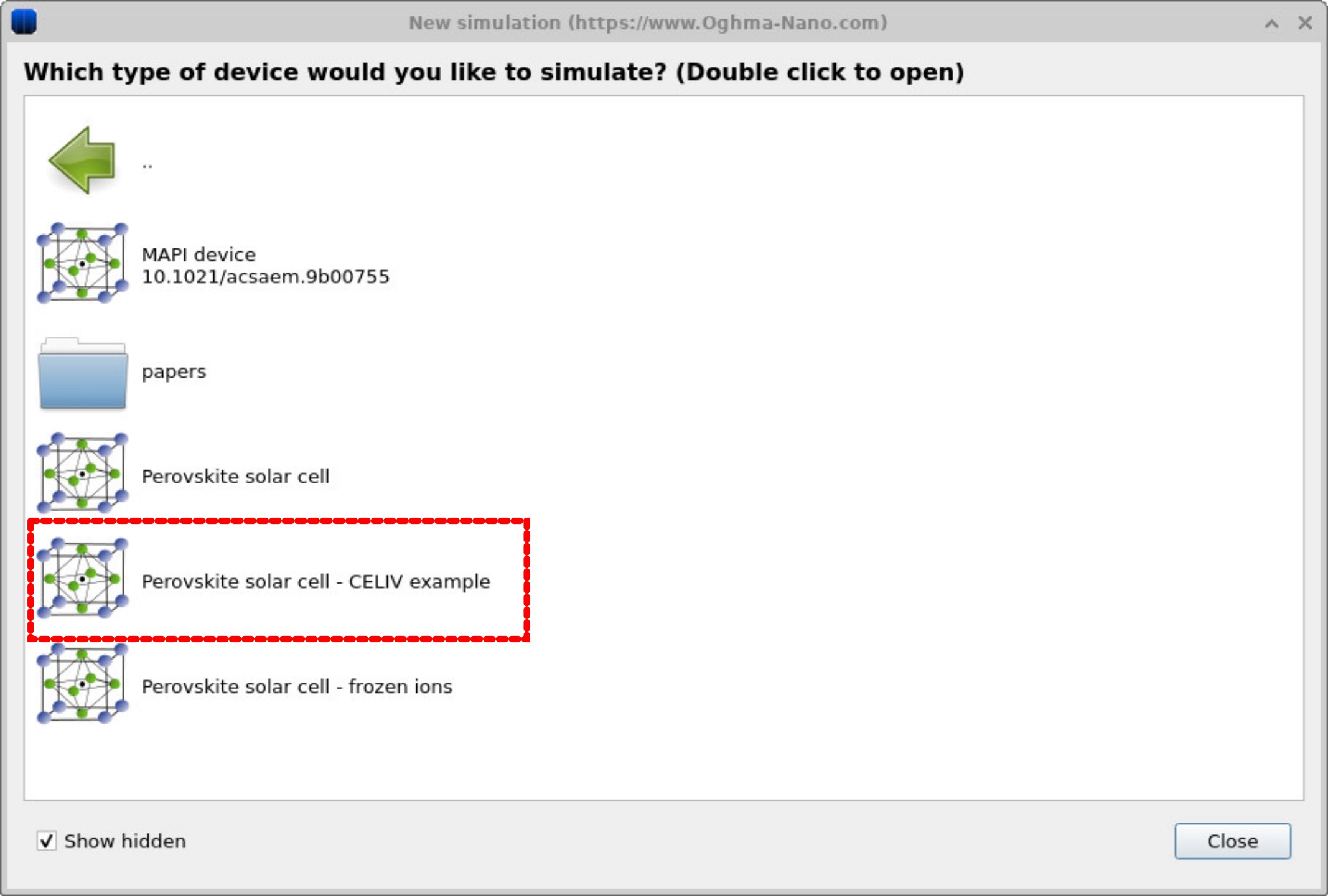
点击 新建仿真。这将打开可用器件类型库，如 ?? 所示。双击 钙钛矿电池（红色高亮）以打开钙钛矿示例文件夹。你会看到一系列预设仿真，包括 MAPbI₃ 器件、 钙钛矿太阳能电池，以及专用的 CELIV 演示，如 ?? 所示。在本教程中，选择 钙钛矿太阳能电池——CELIV 示例。出现提示时，将仿真保存到你具有写权限的文件夹中。

OghmaNano 新建仿真窗口显示器件类别，包括钙钛矿电池、OLED、OFET、GaAs 演示、光线追迹以及 FDTD 示例 — *新建仿真* 窗口提供器件类型与示例项目库。双击某个类别可打开预配置的仿真——例如此处高亮的 **钙钛矿电池** 文件夹。

OghmaNano 钙钛矿太阳能电池示例列表，显示预配置的 MAPbI₃ 器件、钙钛矿太阳能电池以及 CELIV 示例模板 — 在 *钙钛矿电池* 类别中，你可以选择多种预构建的器件结构，包括 **MAPbI₃** 示例、通用的 **钙钛矿太阳能电池**，以及专用的 **CELIV 示例**。在本教程中，选择 CELIV 模板以探索 OghmaNano 如何模拟电荷抽取瞬态。

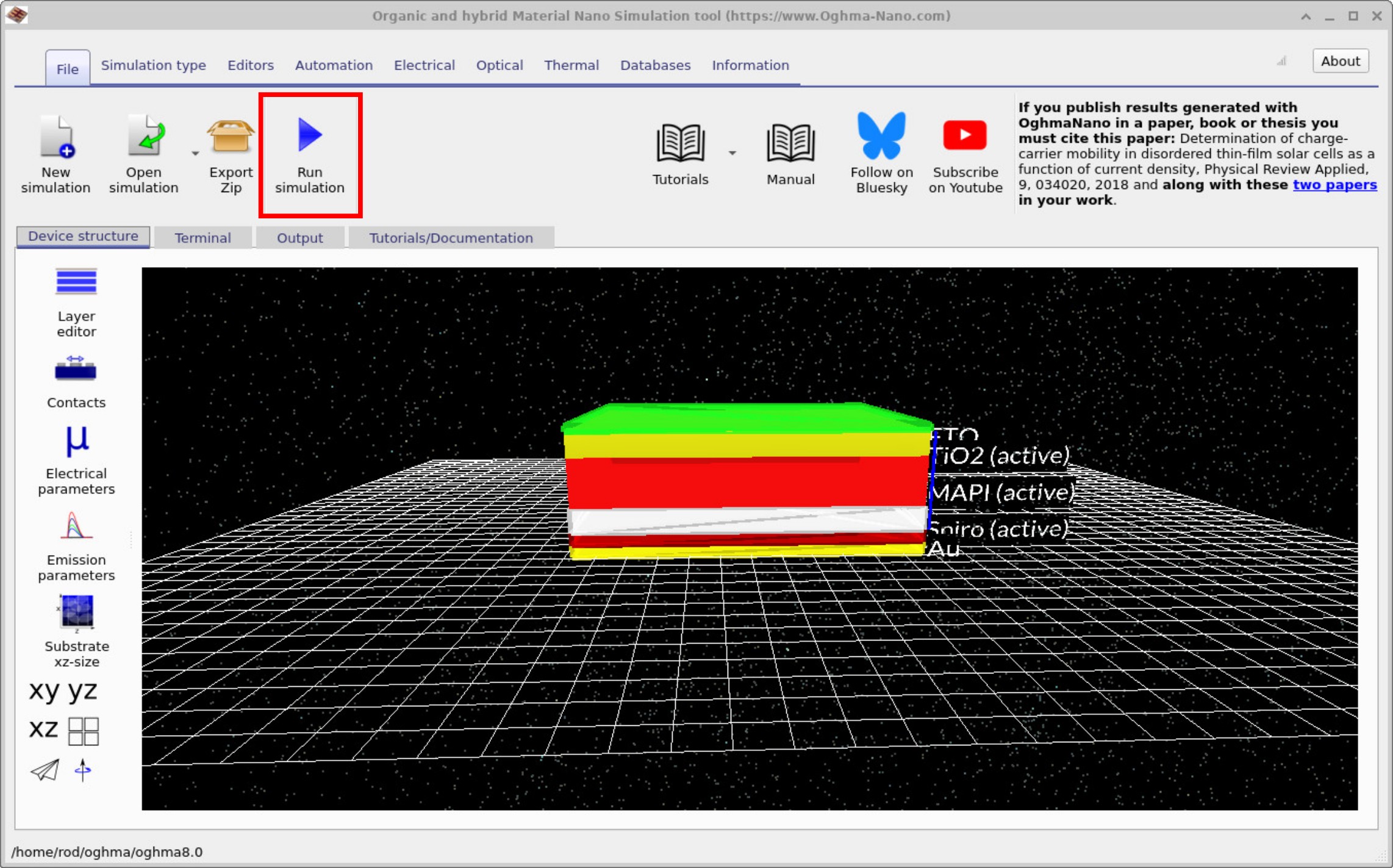
选择 钙钛矿太阳能电池——CELIV 示例 后，将打开主仿真窗口（见 ??）。要开始计算，点击 运行仿真（蓝色播放图标）或按 F9。随后 OghmaNano 将求解含时的 drift–diffusion 方程并生成 CELIV 瞬态。

OghmaNano 主仿真界面显示运行仿真按钮，以及带有 FTO、TiO₂、MAPbI₃、Spiro 和 Au 标注层的 3D 钙钛矿太阳能电池堆叠。 — *OghmaNano* 的主界面。工具栏提供对创建/打开仿真、导出结果以及运行求解器等操作的快捷访问。 3D 视图显示器件结构（此处为 **FTO / TiO₂ / MAPbI₃ / Spiro / Au**）。点击高亮的 **运行仿真** 按钮（或按 `F9`）开始。

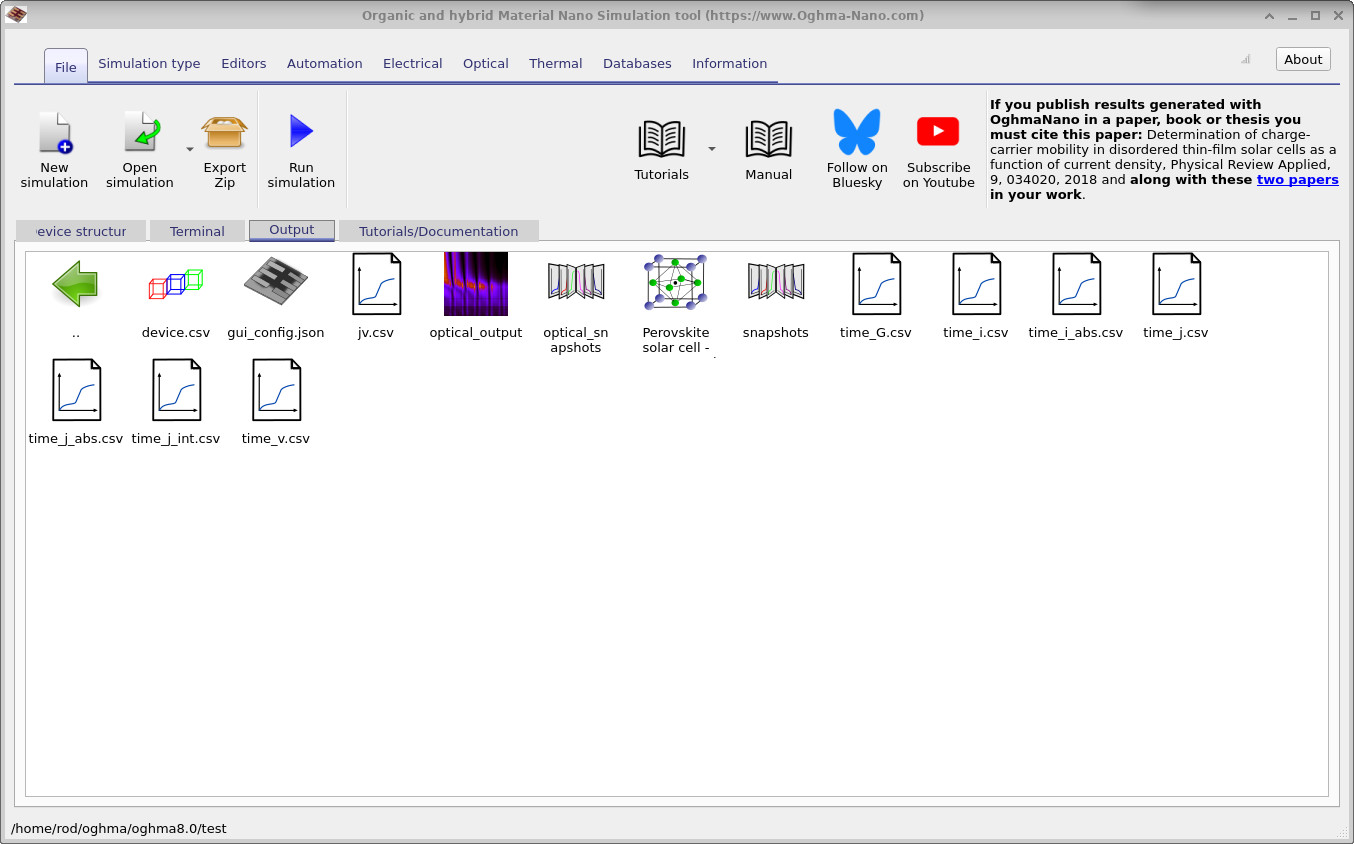
OghmaNano Output 选项卡显示工作目录及 CELIV 结果文件，例如 jv.csv、time_j.csv、time_v.csv 和光学输出。 — *OghmaNano* 的 *Output* 选项卡。在此可浏览当前 CELIV 仿真的工作目录。典型结果包括 `jv.csv`（JV 曲线数据）、`time_j.csv`（抽取电流随时间）、 `time_v.csv`（施加电压随时间）以及 `optical_output`（场分布）。双击任一文件即可在内置绘图工具中查看相应结果。

第 5 步：查看 CELIV 结果

施加电压随时间：CELIV 电压程序显示平坦的预偏置、到 Vr 的线性斜坡，然后返回到初始偏置。 — 用于 CELIV 的施加电压斜坡。

抽取电流密度随时间：CELIV 瞬态显示电容基线与由载流子抽取导致的尖锐峰，随后在返回过程中出现一个相反符号的峰。 — 仿真的 CELIV 电流瞬态。

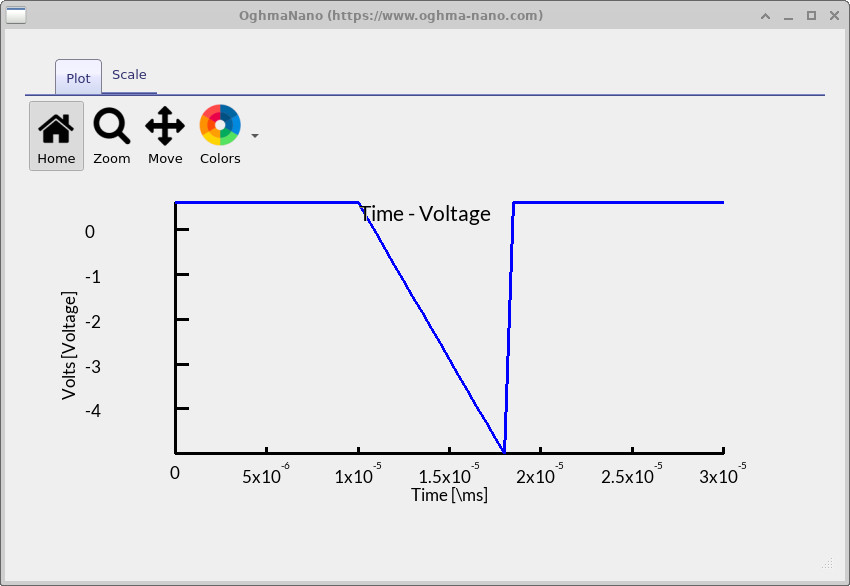
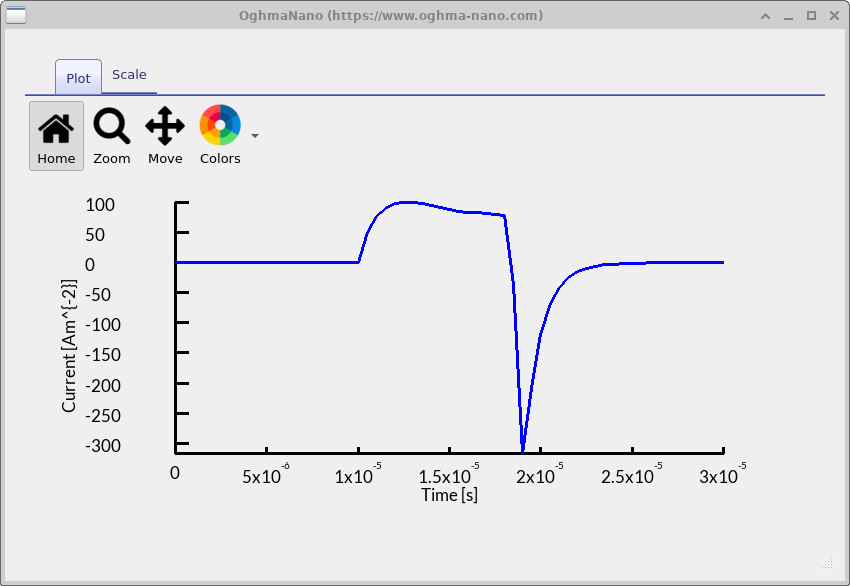
打开 Output 选项卡（??）并双击 time_v.csv。这会绘制施加的电压程序—— CELIV 斜坡——如 ?? 所示。接着，双击 time_j.csv 以显示抽取电流瞬态，如 ?? 所示。你会注意到该瞬态具有熟悉的 CELIV 形状，但看起来 **倒置**：在 OghmaNano 的符号约定中，离开器件的电流为负。施加 ?? 中的斜坡时，电荷被从器件中拉出，因此器件输出负电流（抽取峰）。随后出现的相反符号峰（在 ?? 中为正）发生在偏置返回时：当瞬态回到初始状态后，电荷迅速回流进入器件。

CELIV 抽取电流瞬态，符号取反以匹配常规形式。图中显示来自器件电容的基线以及对应载流子抽取的尖锐正峰。 — 将符号取反后的仿真 CELIV 电流瞬态，以显示通常的正向抽取峰。电容贡献形成基线，而主峰对应载流子被从器件中拉出。

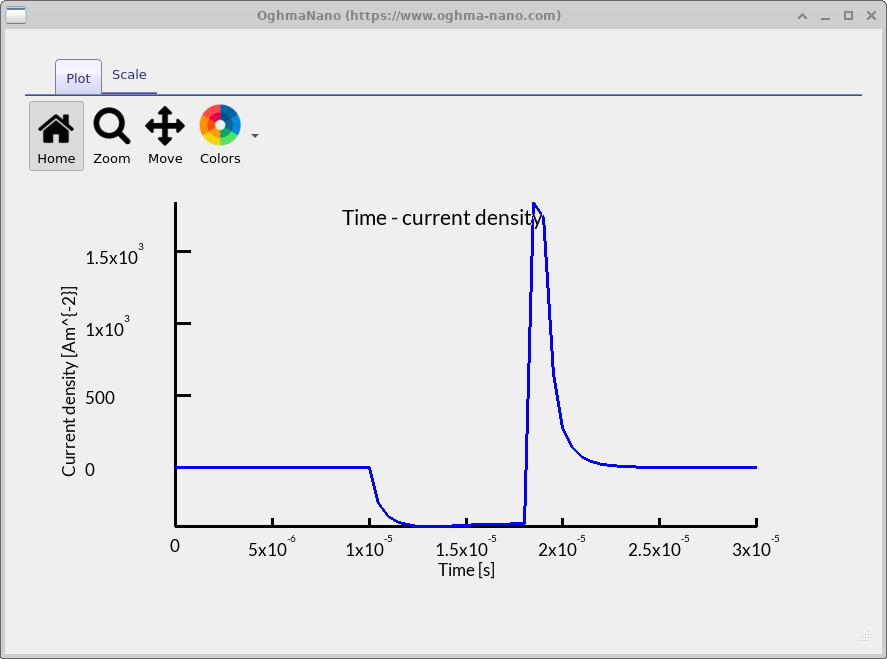
?? 中的曲线表示将仿真电流乘以 –1 后的 CELIV 瞬态，以匹配实验中常用的常规展示方式。在这种形式下，基线对应于器件的几何电容，而尖锐的正峰表示在施加电压斜坡期间抽取可移动电荷载流子。该峰的幅值与出现时间是用于确定载流子迁移率与密度的关键量。以这种常规方向呈现瞬态更便于将 OghmaNano 仿真与已发表的 CELIV 测量直接比较。要提取迁移率，确定电流达到最大值的时间（\(t_\text{max}\)）并将该值代入 CELIV 迁移率方程 \(\mu = \tfrac{2d^2}{3At_\text{max}^2}\)，其中 \(d\) 为有源层厚度， \(A\) 为施加的电压斜坡速率。

div style="clear: both;">

🧪 示例计算： 从 ?? 读取 CELIV 峰值时间并估算迁移率。假设有源层厚度为 d = 600 nm，电压斜坡速率为 A = 5 × 10⁵ V/s，测得峰值时间为 t_max = 3 µs。你得到的迁移率是多少？

显示答案

使用 CELIV 关系式 \[ \mu = \frac{2 d^{2}}{3 A t_{\text{max}}^{2}} \] 其中 \(d = 600\times10^{-9}\,\mathrm{m}\)，\(A = 5\times10^{5}\,\mathrm{V\,s^{-1}}\)， \(t_{\text{max}} = 3\times10^{-6}\,\mathrm{s}\)。

\[ \mu = \frac{2(600\times10^{-9})^{2}}{3\,(5\times10^{5})\,(3\times10^{-6})^{2}} \approx 5.3\times10^{-8}\ \mathrm{m^{2}\,V^{-1}\,s^{-1}} \] 转换为 \(\mathrm{cm^{2}\,V^{-1}\,s^{-1}}\)（\(1\ \mathrm{m^{2}} = 10^{4}\ \mathrm{cm^{2}}\)）： \[ \mu \approx 5.3\times10^{-4}\ \mathrm{cm^{2}\,V^{-1}\,s^{-1}}. \]

该数值处于无序有机半导体文献中常报告的典型范围。（如果你的 \({t_\text{max}}\) 随斜坡速率或照明变化，你会看到 \(\mu\) 也相应变化。）

👉 下一步： 进入下一节 CELIV（C-LIV）仿真内容 — 第 B 部分 — 我们将：调整电压斜坡速率，试验照明强度，并探索改变电子/空穴迁移率如何重塑 CELIV 瞬态。